
Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app. We also provide extensive NCERT solutions, sample papers, NEET, JEE Mains, BITSAT previous year papers, which makes us a one-stop solution for all resources. Physics Wallah is India's top online ed-tech platform that provides affordable and comprehensive learning experience to students of classes 6 to 12 and those preparing for JEE and NEET exams. When a body is displaced from its equilibrium it is acted upon by a restoring force (or torque) which always acts to accelerate the body in the direction of its equilibrium position as shown in the figure. The force acting on the body at any position is given by In terms of energy, we can say that a particle executing harmonic motion moves back and forth about a point at which the potential energy is minimum (equilibrium position). Since F = ma, therefore, the force acting on the body also varies in magnitude and direction with time. When a body oscillates along a straight line within two fixed limits its displacement x changes periodically in both magnitude and direction its velocity v and acceleration a also vary periodically in magnitude and direction, shown in fig.(13.1).
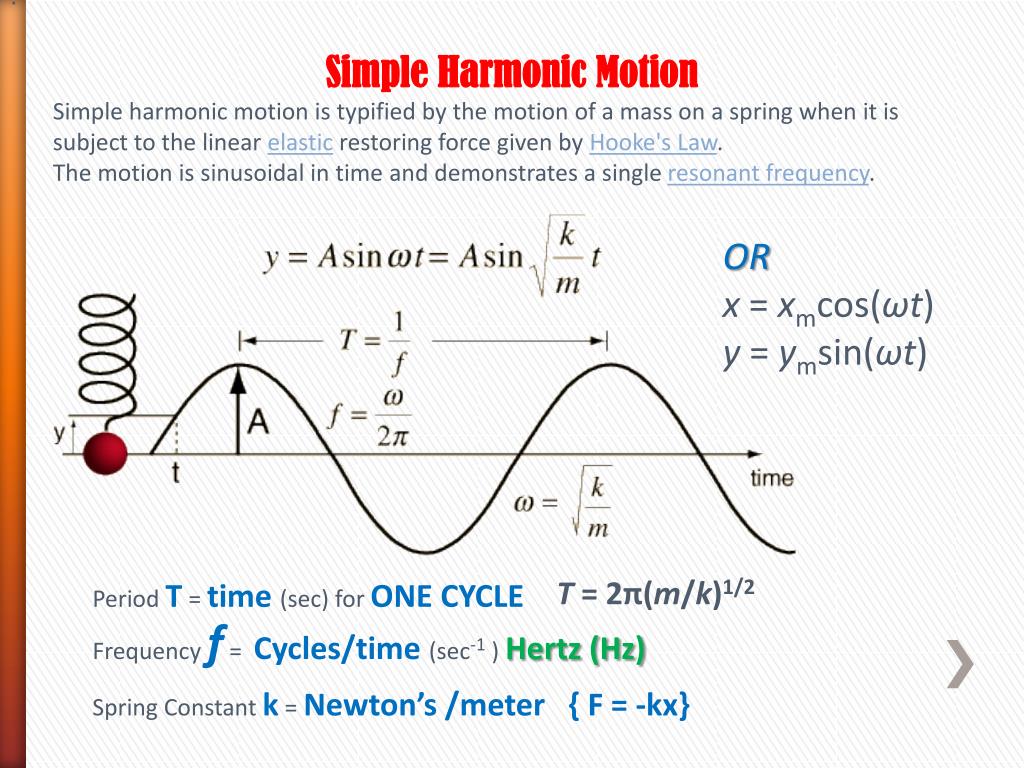
The displacement (linear or angular) of an oscillating particle is its distance (linear or angular) from the equilibrium position at any instant. At the equilibrium position no net force (or torque) acts on the oscillating body. In mechanical oscillations a body oscillates about its mean position which is also its equilibrium position. The SI unit of frequency is s-1 or Hz (hertz) The frequency is related to the time period as The frequency of oscillations is the number of cycles of vibrations of a body completed in one second. The time period of oscillations is defined as the time between two successive identical positions passed by the body in the same direction. The amplitude of oscillations is the maximum displacement of a vibrating body from the position of equilibrium. The basic quantities characterizing a periodic motion are the amplitude, period and frequency of vibrations.

Oftenly, the displacement of a particle in periodic motion can always be expressed in terms of sine and cosine functions. The time calculation calculates the first time the motion reaches the specified displacement, i.e., the time during the first period.Any motion, which repeats itself in equal intervals of time is called periodic motion. The angular frequency calculation assumes that the motion is in its first period and therefore calculates the smallest value of angular frequency which will match the other parameters. Default values will be entered for any missing data, but those values may be changed and the calculation repeated. The motion is described by Displacement = Amplitude x sin ( angular frequency x time) yĪny of the parameters in the motion equation can be calculated by clicking on the active word in the motion relationship above. Then the frequency is f = Hz and the angular frequency = rad/s. The motion equations for simple harmonic motion provide for calculating any parameter of the motion if the others are known.

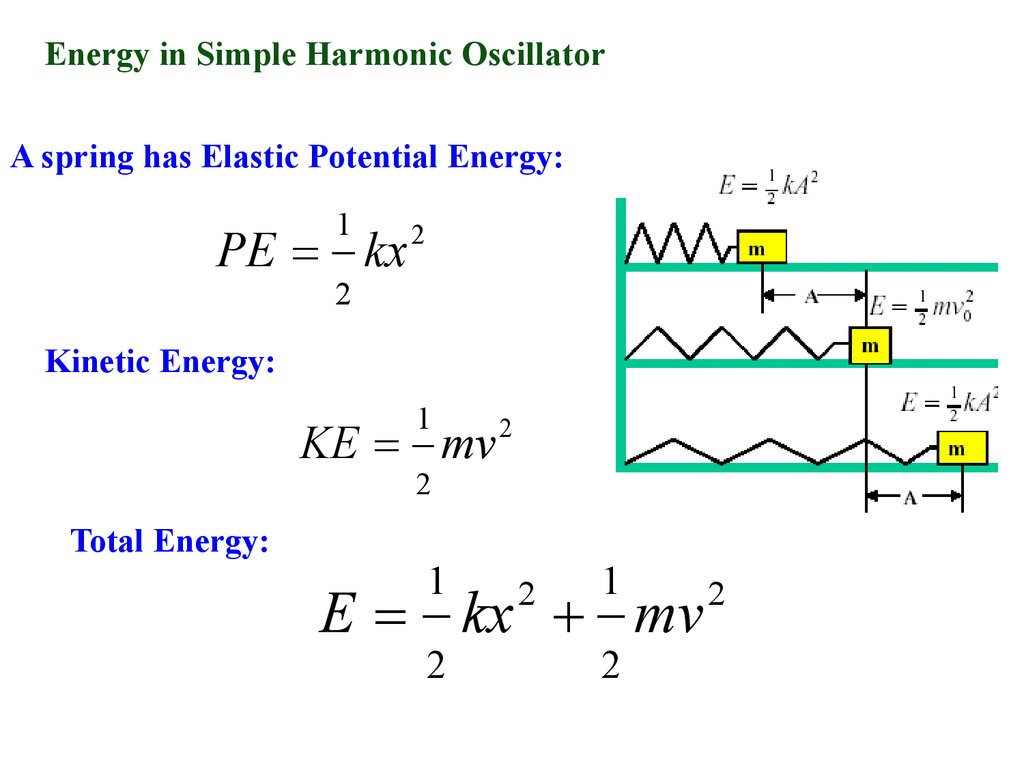
The total energy for an undamped oscillator is the sum of its kinetic energy and potential energy, which is constant at The velocity and acceleration are given by The motion equation for simple harmonic motion contains a complete description of the motion, and other parameters of the motion can be calculated from it. The motion is sinusoidal in time and demonstrates a single resonant frequency. Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. Simple Harmonic Motion Simple Harmonic Motion


 0 kommentar(er)
0 kommentar(er)
